The world has been recognizing the crucial importance of mathematics from the very first day of existence. Daily life activities involve mathematical strategies to an extent that every minor task includes its role, whether it is counting cash, calculating time, cooking dishes, or even writing this article. But as simple it seems in the words; its learning is a complex task for the new learners. The school days focus on cramming these formulas in young minds without knowing its purpose to learn. They are taught to apply formulas as directed by their instructors, whether they like it or not, they are pushed to do these activities without any interactive strategy or technique. It is a kind of hard fun that describes the type of learning faced by us nowadays (Clifford & Friensen, 2003). My experience is not much different than the above-said situations. I had witnessed the same learning strategies which were not attractive nor were interesting to encourage learning in young minds. All were just going through the text to get good grades and no intellectual understanding was provided to solve the complex real-life problems. This has resulted in a huge gap between theoretical learning and practical application of the same. Students start feeling bored after some time and the learning process becomes a burden rather than a fun activity. This requires an expert, who can dispense his knowledge of what they know to those who don’t know (Jardine & Kraemer, 2005). This whole scenario has made a burning issue of teaching mathematical formulas in an interactive way so that learning can be enhanced among the young generation. A lot of pupils are walking away from studying mathematics subjects which is a matter of real concern in this ever-growing technical world. Not only the learning practices, but there is a need to involve updated technology to foster the students’ learning, like the use of smart boards, 3 D modeling structures, puzzle games, and outdoor activities aimed at understanding the basics of mathematics.
These whole things have led to a discussion about the requirements for ensuring better understanding among the students;
- What are the resources required for implementing the interactive approach of learning to mathematics?
- What type of logic and patterns should be used, like games and puzzles?
- How to analyze and apply mathematical ideas to make connections using your own personal experiences?
- Estimate and then figure out what is the best possible approaches to reach the conclusion?
- Effective demonstration and implementation of strategies and then measuring its effectiveness, if it is feasible or not?
Other queries include the feedback and improvement of strategies, reflection, justification of the new methodology, and so on.
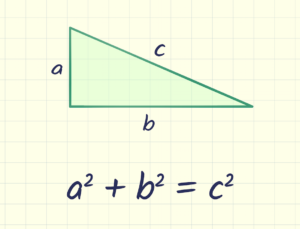
I have chosen this area to foster the learning process among young minds towards the understanding of mathematical formulas. I aimed at grade 8 BC curriculum to get an insight of the inquiry methodology, so that the areas needed to be covered can be assured, such as Pythagorean theorem, calculating areas of geometrical shapes and finding out the relation of probability factor and its real-life meaning in the complex tasks ( BC Curriculum, n.d.). So, the focus is laid on developing new techniques of providing knowledge to the students so that they feel connected with the curriculum and motivate themselves towards better learning. This is equally true when I found myself lucky enough to grab the understanding of mathematical techniques with just virtual assumptions of the taught formulas and figures, which cannot be imagined building up in everyone’s mind. All the learnings were just in the words and no connection was present between class learning and the actual happenings in the outside world. So, this issue encourages me to develop new strategies according to the kind of mathematical strategy and then develop its implementation procedure in that scenario. Whenever I face any new formula or strategies, my mind starts developing new methodology without any kind of formal planning or draft layout. This automatic elaboration of ideas is the motivator behind my ongoing Inquiry procedure as the whole process of my Inquiry is a deep interest in building up new formula-learning field strategies. Watching out students developing new ways to solve complex problems, encourages creativity, and thus assist in the further learning process.
My inquiry template will include some core concepts of mathematical insight and understanding of the basics of formulas. Its structure is aimed at the intellectual understanding of the formulas and then finding out how they are relevant and useful in life skills. The inquiry will include reasoning and proofing by developing required conjectures and then distinguishing different implications of mathematical strategies. The next step is aimed at problem-solving through planning and then sub-planning to identify different problems and their variation on practical grounds. Modeling is the next step which is focused on developing strategies according to the diversity and comparing it with other models to find out a working technique. Basically, it is a hit and trial process and includes a lot of errors and practices for successful implementation.
The ideas for problem-solving can be different from not limited to one criterion which results in different methodologies applied by the students. One can solve geometry areas by his or her own imaginations from the drawn figures. Mathematization is quite different from merely applying teacher provided lessons, as students describe a situation in a way in which relationships are more apparent and clearer. Like, when students are taught algebraic problems, they imagine the same by counting chopsticks for summation or subtraction. But we can’t imagine the same from every student as some do it just in their minds. The same is true for the Pythagorean theorem, some develop their calculation from the square roots while others draw an imaginary projection of the stated problem. Things vary from person to person and tasks also.
The idea of Inquiry will focus on developing an intellectual understanding of mathematical formulas with the involvement of different technical resources aimed at making the learning process interactive and easy for the students. Tasks will include playground activities, puzzles, and other fun learning to engage more and more students in the learning process. The whole process will be aimed at finding out the different strategies, the scope of the possible solutions, and their feasibility in the long run for effective running.